Введение в анализ, синтез и моделирование систем
Меры информации в системе
В предыдущей лекции было отмечено, что информация может пониматься и интерпретироваться в различных проблемах, предметных областях по-разному. Вследствие этого, имеются различные подходы к определению измерения информации и различные способы введения меры количества информации.
Количество информации - числовая величина, адекватно характеризующая актуализируемую информацию по разнообразию, сложности, структурированности (упорядоченности), определенности, выбору состояний отображаемой системы.
Если рассматривается некоторая система, которая может принимать одно из n возможных состояний, то актуальной задачей является задача оценки этого выбора, исхода. Такой оценкой может стать мера информации (события).
Мера, как было сказано выше, - непрерывная действительная неотрицательная функция, определенная на множестве событий и являющаяся аддитивной (мера суммы равна сумме мер).
Меры могут быть статические и динамические, в зависимости от того, какую информацию они позволяют оценивать: статическую (не актуализированную; на самом деле оцениваются сообщения без учета ресурсов и формы актуализации) или динамическую (актуализированную т.е. оцениваются также и затраты ресурсов для актуализации информации).
Ниже мы не всегда будем, в основном, для большей убедительности и большего содержательного понимания, проводить четкие математические границы между понятиями "количество информации" и "мера количества информации", но строгому читателю необходимо все время задавать достаточно важные вопросы: о количестве информации или о мере информации в конкретной последовательности событий идет речь? о детерминированной или стохастической информации идет речь? какова мера измерения количества информации и насколько она адекватна?
1. Мера Р. Хартли. Пусть имеется N состояний системы S или N опытов с различными, равновозможными, последовательными состояниями системы. Если каждое состояние системы закодировать, например, двоичными кодами определенной длины d, то эту длину необходимо выбрать так, чтобы число всех различных комбинаций было бы не меньше, чем N.
Наименьшее число, при котором это возможно, называется мерой разнообразия множества состояний системы и задается формулой Р. Хартли: H=klogаN, где k - коэффициент пропорциональности (масштабирования, в зависимости от выбранной единицы измерения меры), а - основание системы меры.
Если измерение ведется в экспоненциальной системе, то k=1, H=lnN (нат); если измерение было произведено в двоичной системе, то k=1/ln2, H=log2N (бит); если измерение было произведено в десятичной системе, то k=1/ln10, H=lgN (дит).
Пример. Чтобы узнать положение точки в системе из двух клеток т.е. получить некоторую информацию, необходимо задать 1 вопрос ("Левая или правая клетка?"). Узнав положение точки, мы увеличиваем суммарную информацию о системе на 1 бит (I=log2 2). Для системы из четырех клеток необходимо задать 2 аналогичных вопроса, а информация равна 2 битам (I=log24). Если же система имеет n различных состояний, то максимальное количество информации будет определяться по формуле: I=log2n.
Справедливо утверждение Хартли: если в некотором множестве X={x1, x2, ..., xn} необходимо выделить произвольный элемент xi

Если N - число возможных равновероятных исходов, то величина klnN представляет собой меру нашего незнания о системе.
По Хартли, для того, чтобы мера информации имела практическую ценность, она должна быть такова, чтобы отражать количество информации пропорционально числу выборов.
Пример. Имеются 192 монеты. Известно, что одна из них - фальшивая, например, более легкая по весу. Определим, сколько взвешиваний нужно произвести, чтобы выявить ее. Если положить на весы равное количество монет, то получим 3 независимые возможности: а) левая чашка ниже; б) правая чашка ниже; в) чашки уравновешены. Таким образом, каждое взвешивание дает количество информации I=log23, следовательно, для определения фальшивой монеты нужно сделать не менее k взвешиваний, где наименьшее k удовлетворяет условию log23k

Отсюда, k

Пример. ДНК человека можно представить себе как некоторое слово в четырехбуквенном алфавите, где каждой буквой помечается звено цепи ДНК или нуклеотид. Определим, сколько информации (в битах) содержит ДНК, если в нем содержится примерно 1,5?1023 нуклеотидов (есть и другие оценки этого объема, но мы рассмотрим данный вариант). На один нуклеотид приходится log2(4)=2 (бит) информации. Следовательно, структура ДНК в организме человека позволяет хранить 3?1023 бит информации. Это вся информация, сюда входит и избыточная. Реально используемой - структурированной в памяти человека информации, - гораздо меньше. В связи с этим, заметим, что человек за среднюю продолжительность жизни использует около 5-6% нейронов (нервных клеток мозга - "ячеек ОЗУ человека"). Генетический код - чрезвычайно сложная и упорядоченная система записи информации. Информация, заложенная в генетическом коде (по учению Дарвина), накапливалась многие тысячелетия. Хромосомные структуры - своеобразный шифровальный код, при клеточном делении создаются копии шифра, каждая хромосома - удваивается, в каждой клетке имеется шифровальный код, при этом каждый человек получает, как правило, свой набор хромосом (код) от матери и от отца. Шифровальный код разворачивает процесс эволюции человека. Вся жизнь, как отмечал Э. Шредингер, "упорядоченное и закономерное поведение материи, основанное ... на существовании упорядоченности, которая поддерживается все время".
Формула Хартли отвлечена от семантических и качественных, индивидуальных свойств рассматриваемой системы (качества информации в проявлениях системы с помощью рассматриваемых N состояний системы). Это основная и положительная сторона формулы. Но имеется основная и отрицательная ее сторона: формула не учитывает различимость и различность рассматриваемых N состояний системы.
Уменьшение (увеличение) Н может свидетельствовать об уменьшении (увеличении) разнообразия состояний N системы. Обратное, как это следует из формулы Хартли (так как основание логарифма больше 1!), - также верно.
2. Мера К. Шеннона. Формула Шеннона дает оценку информации независимо, отвлеченно от ее смысла:

где n - число состояний системы; рi - вероятность (или относительная частота) перехода системы в i-е состояние, причем сумма всех pi равна 1.
Если все состояния равновероятны (т.е. рi=1/n), то I=log2n.
К. Шенноном доказана теорема о единственности меры количества информации. Для случая равномерного закона распределения плотности вероятности мера Шеннона совпадает с мерой Хартли. Справедливость и достаточная универсальность формул Хартли и Шеннона подтверждается и данными нейропсихологии.
Пример. Время t реакции испытуемого на выбор предмета из имеющихся N предметов линейно зависит от log2N: t=200+180log2N (мс). По аналогичному закону изменяется и время передачи информации в живом организме. Один из опытов по определению психофизиологических реакций человека состоял в том, что перед испытуемым большое количество раз зажигалась одна из n лампочек, на которую он должен был указать в ходе эксперимента. Оказалось, что среднее время, необходимое для правильного ответа испытуемого, пропорционально не числу n лампочек, а именно величине I, определяемой по формуле Шеннона, где pi - вероятность зажечь лампочку номер i
Легко видеть, что в общем случае

Если выбор i-го варианта предопределен заранее (выбора, собственно говоря, нет, pi=1), то I=0.
Сообщение о наступлении события с меньшей вероятностью несет в себе больше информации, чем сообщение о наступлении события с большей вероятностью. Сообщение о наступлении достоверно наступающего события несет в себе нулевую информацию (и это вполне ясно: событие всё равно произойдет когда-либо).
Пример. Если положение точки в системе известно, в частности, она - в k-ой клетке, т.е. все рi=0, кроме рk=1, то тогда I=log21=0 и мы здесь новой информации не получаем (как и следовало ожидать).
Пример. Выясним, сколько бит информации несет произвольное двузначное число со всеми значащими цифрами (отвлекаясь при этом от его конкретного числового значения, т.е. каждая из возможных цифр может появиться на данном месте, в данном разряде с одинаковой вероятностью). Так как таких чисел может быть всего 90 (10-99), то информации будет количество I=log290 или приблизительно I=6,5. Так как в таких числах значащая первая цифра имеет 9 значений (1-9), а вторая - 10 значений (0-9), то I=log290=log29+log210. Приблизительное значение log210 равно 3,32. Итак, сообщение в одну десятичную единицу несет в себе в 3,32 больше информации, чем в одну двоичную единицу (чем log22=1), а вторая цифра, например, в числе аа, несет в себе больше информации, чем первая (если цифры а обоих разрядов неизвестны; если же эти цифры а известны, то выбора нет и информация равна нулю).
Если в формуле Шеннона обозначить fi=-nlog2 pi, то получим, что I можно понимать как среднеарифметическое величин fi.
Отсюда, fi можно интерпретировать как информационное содержание символа алфавита с индексом i и величиной pi вероятности появления этого символа в сообщении, передающем информацию.
Пример. Пусть рассматривается алфавит из двух символов русского языка - "к" и "а". Относительные частоты встречаемости этих букв в частотном словаре русского языка равны соответственно p1=0.028, p2=0.062. Возьмем произвольное слово p длины N из k букв "к" и m (k+m=N) букв "а" над этим алфавитом. Число всех таких возможных слов, как это следует из комбинаторики, равно n=N!/(k! m!). Оценим количество информации в таком слове: I=log2n=lnn/ln2=log2e[lnN!-lnk!-lnm!]. Используя известную формулу Стирлинга (эта формула, как известно из математического анализа, достаточно точна при больших N, например, при N>100) - N!?(N/e)N), а точнее, ее важное следствие, - lnN!?N(lnN-1), получаем оценку количества информации (в битах) на 1 символ любого слова:
I1=I/N?(log2e/N)[(k+m)(lnN -1) - k(ln k-1) - m(ln m-1)]= =(log2e/N)[k ln(N/k) - m ln(N/m)]= = - log2e[(k/N) ln(k/N) + (m/N) ln(m/N)]


В сообщении 4 буквы "a", 2 буквы "б", 1 буква "и", 6 букв "р". Определим количество информации в одном таком ( из всех возможных) сообщений. Число N различных сообщений длиной 13 букв будет равно величине: N=13!/(4!?2!?1!?6!)=180180. Количество информации I в одном сообщении будет равно величине: I=log2(N)=log2180180?18 (бит).
Если k - коэффициент Больцмана, известный в физике как k=1.38?10-16 эрг/град, то выражение

в термодинамике известно как энтропия, или мера хаоса, беспорядка в системе. Сравнивая выражения I и S, видим, что I можно понимать как информационную энтропию (энтропию из-за нехватки информации о/в системе).
Л. Больцман дал статистическое определение энтропии в 1877 г. и заметил, что энтропия характеризует недостающую информацию. Спустя 70 лет, К. Шеннон сформулировал постулаты теории информации, а затем было замечено, что формула Больцмана инвариантна информационной энтропии, и была выявлена их системная связь, системность этих фундаментальных понятий.
Важно отметить следующее.
Нулевой энтропии соответствует максимальная информация. Основное соотношение между энтропией и информацией:
I+S(log2e)/k=const или в дифференциальной форме
dI/dt= -((log2e)/k)dS/dt.При переходе от состояния S1 с информацией I1 к состоянию S2 с информацией I2 возможны случаи:
- S1 < S2 (I1 >I2) - уничтожение (уменьшение) старой информации в системе;
- S1 = S2 (I1 = I2) - сохранение информации в системе;
- S1 > S2 (I1 < I2) - рождение новой (увеличение) информации в системе.
Теория Шеннона разработана как теория передачи данных по каналам связи, а мера Шеннона - мера количества данных и не отражает семантического смысла.
Увеличение (уменьшение) меры Шеннона свидетельствует об уменьшении (увеличении) энтропии (организованности) системы. При этом энтропия может являться мерой дезорганизации систем от полного хаоса (S=Smax) и полной информационной неопределенности (I=Imin) до полного порядка (S=Smin) и полной информационной определённости (I=Imax) в системе.
3. Термодинамическая мера. Информационно-термодинамический подход связывает величину энтропии системы с недостатком информации о внутренней структуре системы (не восполняемым принципиально, а не просто нерегистрируемым). При этом число состояний определяет, по существу, степень неполноты наших сведений о системе.
Пусть дана термодинамическая система (процесс) S, а Н0, Н1 - термодинамические энтропии системы S в начальном (равновесном) и конечном состояниях термодинамического процесса, соответственно. Тогда термодинамическая мера информации (негэнтропия) определяется формулой:
Н(Н0,Н1)=Н0 - Н1.Эта формула универсальна для любых термодинамических систем. Уменьшение Н(Н0,Н1) свидетельствует о приближении термодинамической системы S к состоянию статического равновесия (при данных доступных ей ресурсах), а увеличение - об удалении.
Поставим некоторый вопрос о состоянии термодинамической системы. Пусть до начала процесса можно дать p1 равновероятных ответов на этот вопрос (ни один из которых не является предпочтительным другому), а после окончания процесса - p2 ответов. Изменение информации при этом:
?I=k ln(p1 / p2)=k (ln p1 - ln p2 ).Если p1>p2 (?I>0) - идет прирост информации, т.е. сведения о системе стали более определенными, а при p1<p2 (?I<0) - менее определенными. Универсально то, что мы не использовали явно структуру системы (механизм протекания процесса).
Пример. Предположим, что имеется развивающаяся социально-экономическая система с числом состояний 10, которая в результате эволюции развилась до системы с числом состояний 20.
Нас интересует вопрос о состоянии некоторого составного элемента системы (например, предприятия). В начале мы знали ответ на вопрос и поэтому p1=1 (lnp1=0). Число ответов было пропорционально величине [ln10]. После развития мы знаем уже микроэкономическое состояние, т.е. изменение информации о состоянии системы равно ?I = -kln(20/10) = -kln2 (нат).
Пример. Предположим, что имеется термодинамическая система - газ в объеме V , который расширяется до объема 2V (рис. 6.1).
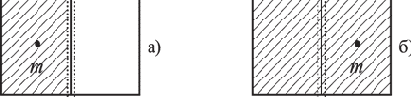
Рис. 6.1. Газ объема V (a) расширяемый до 2V (б)
Нас интересует вопрос о координате молекулы m газа. В начале (а) мы знали ответ на вопрос и поэтому p1=1 (lnp1=0). Число ответов было пропорционально lnV. После поднятия заслонки мы уже знаем эту координату (микросостояния), т.е. изменение (убыль) информации о состоянии системы будет равно
?I = -k ln(2V /V) = -k ln 2 (нат).Мы получили известное в термодинамике выражение для прироста энтропии в расчете на одну молекулу, и оно подтверждает второе начало термодинамики. Энтропия - мера недостатка информации о микросостоянии статической системы.
Величина ?I может быть интерпретирована как количество информации, необходимой для перехода от одного уровня организации системы к другому (при ?I>0 - более высокому, а при ?I>0 - более низкому уровню организации).
Термодинамическая мера (энтропия) применима к системам, находящимся в тепловом равновесии. Для систем, далеких от теплового равновесия, например, живых биологических систем, мера-энтропия - менее подходящая.
4. Энергоинформационная (квантово-механическая) мера. Энергия (ресурс) и информация (структура) - две фундаментальные характеристики систем реального мира, связывающие их вещественные, пространственные, временные характеристики. Если А - именованное множество с носителем так называемого "энергетического происхождения", а В - именованное множество с носителем "информационного происхождения", то можно определить энергоинформационную меру f: A

Отношение именования должно отражать механизм взаимосвязей физико-информационных и вещественно-энергетических структур и процессов в системе.
Отметим, что сейчас актуальнее говорить о биоэнергоинформационных мерах, отражающих механизм взаимосвязей биофизико-информационных и вещественно-энергетических структур и процессов в системе.
Пример. Процесс деления клеток сопровождается излучением квантов энергии с частотами приблизительно до N=1.5?1015 гц. Этот спектр можно воспринимать как спектр функционирования словарного запаса клетки как биоинформационной системы. С помощью этого спектра можно закодировать до 1015 различных биохимических реакций, что примерно в 107 раз больше количества реакций реально протекающих в клетке (их количество - примерно 108), т.е. словарный запас клетки избыточен для эффективного распознавания, классификации, регулирования этих реакций в клетке. Количество информации на 1 квант энергии: I=log21015?50 бит. При делении клеток количество энергии, расходуемой на передачу 50 бит информации равно энергии кванта (h - постоянная Планка, n - частота излучения):
E=h?=6,62?10-27 (эрг/cек) ? 0,5?1015 (сек-1) =3,3?10-12 (эрг).При этом на 1 Вт мощности "передатчика" или на ?=107 эрг/сек. может быть передано количество квантов:
n=?/E=107 (эрг/сек)/(3,3?10-12 (эрг))?3,3?1018 (квант).Общая скорость передачи информации на 1 Вт затрачиваемой клеткой мощности определяется по числу различных состояний клетки N и числу квантов (излучений) m:
V=n log2N=3,3?1018?50?1,6?1020 (бит/сек).Любая информация актуализируется в некоторой системе. Материальный носитель любой системы - сообщение, сигнал. Любая актуализация сопровождается изменением энергетических свойств (изменением состояния) системы. Наши знания (а, следовательно, и эволюция общества) простираются на столько, на сколько углубляется информация и совершенствуется возможность ее актуализации.
5. Другие меры информации. Многими авторами в последнее время рассматриваются различные количественные меры для измерения смысла информации, например, мера, базирующаяся на понятии цели (А.
Харкевич и другие); мера, базирующаяся на понятии тезаурус Т=<X,Y,Z>, где X, Y, Z - множества, соответственно, имен, смыслов и значений (прагматики) этих знаний (Ю. Шрейдер и другие); мера сложности восстановления двоичных слов (А. Колмогоров и другие); меры апостериорного знания (Н. Винер и другие); мера успешности принятия решения (Н. Моисеев и другие); меры информационного сходства и разнообразия и другие способы, подходы к рассмотрению мер информации.
Пример. В качестве меры (Колмогорова) восстановления двоичного слова y по заданному отображению f и заданным двоичным словам x из непустого множества X можно взять H(f,y)=min|x|, x

Пример. Если априори известно, что некоторая переменная лежит в интервале (0;1), и апостериори, что она лежит в интервале (a;b)

Пример. В биологических науках широко используются так называемые индексные меры, меры видового разнообразия. Индекс - мера состояния основных биологических, физико-химических и др. компонент системы, позволяющая оценить силу их воздействия на систему, состояние и эволюцию системы. Индексы должны быть уместными, общими, интерпретируемыми, чувствительными, минимально достаточными, качественными, широко применяемыми, рациональными. Например, показателем видового разнообразия в лесу может служить
? = vp1 + vp2 +...+vpnгде p1, p2, ..., pn - частоты видов сообщества, обитающих в лесу, n - число видов.