Глава 8.2.1. Переопределенные системы

Начнем разговор о "плохих" СЛАУ с переопределенными условиями, в которых число уравнений больше числа неизвестных.

О постановке задач

Чаще всего СЛАУ с прямоугольной матрицей размера MxN (при M>N, т. е. при числе уравнений большем числа неизвестных) вовсе не имеет решения, т. е. является несовместной, или переопределенной. Листинг 8.6 демонстрирует, что несовместные системы не могут быть решены ни при помощи встроенной функции isolve, ни посредством вычислительного блока Given/Find.
Листинг 8.6. Попытка решения несовместных СЛАУ

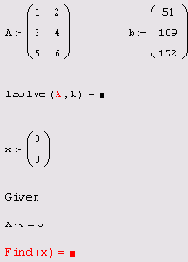
ПРИМЕЧАНИЕ

Конечно, в редких случаях система с прямоугольной матрицей может оказаться совместной (если выбран соответствующий вектор ь), как это показано в листинге 8.7. Любопытно, что итерационный алгоритм блока Given/Find справляется с такой задачей, а алгоритм исключения, заложенный в функции Isolve, — нет.

Листинг 8.7. Пример нахождения решения СЛАУ с прямоугольной матрицей

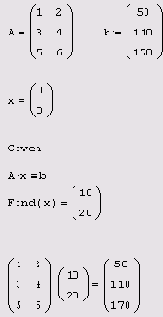
На практике (особенно в последнее время) задачи отыскания решения переопределенных СЛАУ встречаются довольно часто. Приведем простую интерпретацию переопределенной задачи, связанной с обработкой результатов какого-либо эксперимента, например, взвешивания предметов двух типов (для простоты и определенности, совершенно одинаковых яблок и одинаковых груш). Если, согласно постановке задачи, на весы можно положить любое количество предметов любого типа, то модель каждого акта взвешивания представится линейным уравнением, двумя неизвестными в которых будет масса яблока и масса груши. Очевидно, что чем больше взвешиваний мы проведем, тем точнее (в условиях присутствующей в эксперименте погрешности измерений) сможем определить искомые величины.

Обращаясь к числовым примерам листингов 8.6 и 8.7, легко сообразить, что они соответствуют трем актам взвешивания, когда в первый раз на весы кладется одно яблоко и две груши, во второй — три яблока и четыре груши, и в третий — пять яблок и шесть груш. Листинг 8.7 может описывать случай, когда погрешность эксперимента полностью отсутствует, и система трех уравнений с двумя неизвестными оказывается совместной. А листинг 8.6 является примером куда более типичной ситуации, когда погрешность каждого измерения приводит к тому, что итоговая СЛАУ оказывается несовместной, т. е. не имеет никакого точного решения.

ПРИМЕЧАНИЕ

Простой пример с яблоками и грушами является типичным представителем класса обратных задач, подразумевающих, в частности, восстановление неизвестных входных данных эксперимента по наблюдаемым выходным характеристикам (получаемым в условиях наличия погрешности). Для таких задач развиты специальные методы решения, наиболее простой из которых мы приводим в этом и следующем разделах (не останавливаясь на его обосновании, которое потребовало бы привлечения дополнительных соображений из области математической статистики).

Псевдорешение (метод наименьших квадратов)

Напрашивающийся сам собой путь решения нашего простого примера с грушами и яблоками является хорошей иллюстрацией подхода к общей проблеме переопределенных СЛАУ. А именно, вместо точного решения системы уравнений следует организовать поиск такого вектора х, который будет наилучшим образом удовлетворять всем уравнениям, т. е. минимизировать их невязку (расхождение между вектором Aх и вектором правой части СЛАУ b). Поскольку невязка Аx-b является векторной величиной, то, исходя из практических соображений, минимизации надо подвергать ее норму (т. е. скаляр) |Аx-b|. Этот подход позволит, с одной стороны, получить разумное, с физической точки зрения, решение задачи, а, с другой — использовать полезную информацию, заключенную во всех уравнениях.

Таким образом, при интерпретации переопределенных СЛАУ принято искать не точное решение (которого, как уже отмечалось, при данной постановке задачи просто нет), а псевдорешение — вектор, минимизирующий норму невязки системы уравнений. Таким образом, задача решения линейной системы уравнений заменяется задачей отыскания глобального минимума функции f (x) = |Аx-b|. Повторимся еще раз, что, в полном соответствии с обозначениями, принятыми в Mathcad, х — это неизвестный вектор, а символ модуля (две вертикальные черты) означает операцию вычисления нормы (евклидовой длины вектора). Поскольку эта минимизируемая норма зависит от суммы квадратов компонент неизвестного вектора, то процедура поиска псевдорешения является ни чем иным, как реализацией метода наименьших квадратов (МНК).

График функции двух переменных f(x₀,x₁) показан в виде трехмерной поверхности на рис. 8.1, а несколько его сечений в окрестности минимума — на рис. 8.2. Нетрудно сообразить, почему структура функции оказывается именно такой, если вспомнить, что f(x)² является квадратичной формой относительно неизвестных х₀ и x₁ Надо отметить, что если бы наша система имела большее число уравнений, то вычислительная задача соответствующим образом усложнилась бы, т. к. минимизацию следовало бы проводить не по двум, а по большему числу переменных.

Обращаясь к практической стороне дела, следует вспомнить, что для решения задач минимизации невязки системы уравнений (см. главу 6) в Mathcad предусмотрены две встроенные функции — Minerr и Minimize. Применение этих альтернативных средств иллюстрируется листингами 8.8 и 8.9 соответственно. В первом случае используется ключевое слово Given для ввода СЛАУ в матричной форме, а во втором — в явном виде определяется функция f(x), подлежащая минимизации. Обе встроенные функции, как вы помните, применяют итерационные численные алгоритмы, и поэтому требуют ввода начальных значений для всех неизвестных, т. е. нулевой итерации (вторая строка обоих листингов).

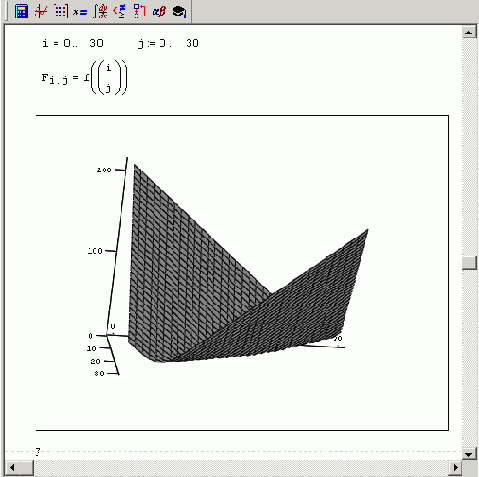
Рис. 8.1. График минимизируемой функции невязки f (х) = | Ах-b|

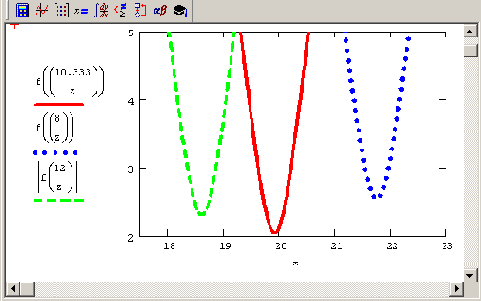
Рис. 8.2. Сечения графика невязки f (х) для трех фиксированных значений х₀

Листинг 8.8. Поиск псевдорешения при помощи функции Minerr

Листинг 8.9. Поиск псевдорешения при помощи функции Minimize

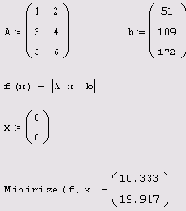
На первый взгляд, удобнее использовать функцию Minerr, поскольку для нее текст Mathcad-программы (листинг 8.8) выглядит более приближенным к изначальной постановке задачи (а именно, найти приближенное решение заданной системы уравнений). Между тем, выбор функции Minerr таит в себе, по крайней мере, две опасности.

Во-первых, сравнивая результаты, можно с недоумением обнаружить, что они абсолютно различны, причем более похож на правильный ответ, выдаваемый функцией Minimize (об этом можно судить, опираясь на соображение ожидаемой близости псевдорешения к решению системы из листинга 8.7, от которого мы отошли лишь немного). Разгадка заключается в особенностях применения численного алгоритма, заложенного в функцию Minerr. По умолчанию решение линейной системы уравнений производится при помощи линейного алгоритма. Чтобы сменить его на нелинейный, необходимо нажатием правой кнопки мыши вызвать из области имени функции контекстное меню и сменить тип метода Linear (Линейный) на один из нелинейных методов Nonlinear (Нелинейный) (рис. 8.3). Однако даже в этом случае, как показывает опыт, наиболее правильный ответ получается только для одного из трех доступных численных алгоритмов.

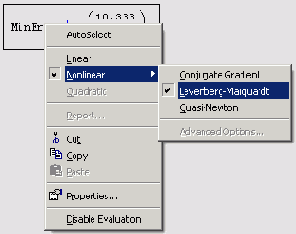
Рис. 8.3. Изменение численного алгоритма для функции Minerr

Во-вторых, приближенное решение СЛАУ посредством вычислительного блока Given/Minerr невозможно при наличии дополнительных условий, выражающих вспомогательную априорную информацию о постановке задачи. В частности, математически более правильным было решать нашу задачу о яблоках и грушах с дополнительным условием положительной определенности компонент неизвестного вектора (поскольку масса фруктов по определению больше нуля). В результате исходная задача сводится к условной минимизации функции f (х), что в Mathcad-программе соответствует появлению дополнительных неравенств после ключевого слова Given (см. пример ниже, решенный в листинге 8. 10). Однако все уравнения и неравенства, предшествующие функции Minerr, будут восприниматься численным процессором Mathcad одинаково, т. е. не в качестве жестких условий, а как выражения, которые должны выполняться лишь с некоторой точностью. В результате найденное решение может вовсе не отвечать условию положительной определенности (этот вопрос обсуждался в разд. 6.2, когда речь шла о задачах оптимизации).

В свете перечисленных проблем применение функции Minimize для поиска псевдорешения СЛАУ выглядит более обоснованным. К слову заметим, что выбор любого из трех нелинейных численных алгоритмов минимизации приводит к одинаковым результатам (листинг 8.9). Функция Minimize годится и для отыскания псевдорешения с дополнительными условиями, выражающими имеющуюся априорную информацию. Соответствующий пример иллюстрирует листинг 8.10, в котором осуществляется поиск псевдорешения СЛАУ, немного отличающейся от рассмотренной выше. Это отличие приводит к тому, что при использовании той же самой методики получается отрицательное решение (третья строка листинга). При добавлении в задачу дополнительных условий результат минимизации оказывается другим (последняя строка листинга 8.10).

ПРИМЕЧАНИЕ

Несколько иной подход к переопределенным системам, для которых имеется дополнительная информация другого типа (а именно, априорная оценка неизвестного вектора х), будет изложен в следующем разделе.

Листинг 8.10. Поиск псевдорешения при наличии априорной информации

Содержание раздела